Soal Kontekstual Berkaitan Perbandingan Trigonometri Pada Segitiga Siku-siku, Sudut Elevasi dan Sudut Depresi
Masalah Kontekstual mengenai Perbandingan Trigonometri pada Segitiga Siku-siku (Sudut Elevasi dan Sudut Depresi)
Pada kesempatan ini kami akan membahas mengenai aplikasinya di kehidupan sehari-hari. Pernahkah anda melihat seseorang mengukur suatu benda yang tinggi menggunakan klinometer? Klinometer adalah alat untuk mengukur sudut kemiringan atau sudut elevasi. Nah! Kita dapat mengetahui tinggi ataupun jarak dari objek tersebut dengan mengetahui sudut elevasi atau sudut depresi serta elemen-elemen yang lainnya.
Apakah sudut elevasi dan sudut depresi itu? Untuk mengetahui definisi kedua macam sudut tersebut, perhatikan ilustrasi berikut.
Sudut Depresi adalah sudut yang terbentuk oleh garis horizontal dengan mata pengamat dengan arah pandang ke bawah.
Masalah Kontekstual mengenai Sudut Elevasi dan Sudut Depresi
1. Sebuah pohon berjarak 130 meter dari seorang pengamat dengan tinggi mata pengamat dari tanah adalah 168 cm. Apabila sudut elevasi yang terbentuk adalah 60° dari mata pengamat ke pucuk pohon, maka tinggi pohon tercebut adalah ….
Jawab:
Agar mudah dalam menyelesaikan masalah di atas, kita harus mampu mentransformasi setiap kalimat dari perrnyataan di atas dalam sebuah gambaran.
Dik: Jarak pengamat ke pohon: 130 meter
Tinggi pengamat: 168 cm = 1,68 meter
Sudut Elevasi 60°
Dit: Tinggi pohon.
Penyelesaian:
Pertama. Buatlah ilustrasinya!
Kedua. Buatlah pemisalan agar memudahkan kita dalam mencari perbandingannya
Misalkan:
Tinggi pohon – tinggi pengamat = t
Jarak pengamat ke pohon =x
Sehingga kita bisa membuat ilustrasi yang lebih sederhana dengan menggunakan segitiga siku-siku
Dari gambar segitiga siku-siku di atas, jika kita menjadikan sudut 60° sebagai acuan, dimana: x adalah sisi samping dan t adalah sisi depan. Sehingga perbandingan yang digunakan adalah
2. Seseorang dari atas sebuah gedung mengamati sebuah toko di seberang jalan. Sudut terbentuk dari pengamatan tersebut adalah 45° . Tinggi gedung 10 lantai itu adalah 52 meter. Berapak jarak antara Gedung dengan toko yang diamati tersebut?
Jawab:
Dik : Tinggi Gedung = 52 meter
Sudut depresi = 45°
Dit : Jarak antara Gedung dengan toko
Penyelesaian:
Sama halnya dengan Langkah nomor 1, buatlah ilustrasi dan misalkan masalah di atas. Berikut ilustrasi sederhana mengenai jarak Gedung dan toko
Dari gambaran segitiga siku-siku di atas diketahui bahwa: x adalah sisi depan dan t adalah sisi sampingnya. Sehingga diperoleh sebagai berikut:
3. Dua orang siswa yang tingginya sama yaitu 160 cm, sedang berdiri menghadap tiap bendera. Siswa pertama berada 10 meter di depan siswa kedua. Jika sudut elevasi yang terbentuk pada siswa pertama dan kedua terhadap puncak tiang bendera berturut-turut adalah 60º dan 30º , maka tinggi tiang bendera tersebut adalah ….
Jawab:
Dik :
Tinggi pengamat : 160 cm = 1,6 meter
Jarak siswa satu dengan yang lainnya : 10 meter
Sudut elevasi Siswa I terhadap puncak bendera : 60º
Sudut elevasi siswa II terhadap puncak bendera : 30º
Dit : Tinggi tiang bendera :
Penyelesaian:
Pertama. Buatlah ilustrasinya
Nah, pada kasus ini, kita terlebih dahulu dapat menambahkan ilustrasi sederhana berupa gambaran segitiga yang dapat memudahkan kita dalam memberikan pemberian nama pada titik-titiknya.
Misalkan:
AC : tinggi tiang bendera
DG : Tinggi siswa I
EF : Tinggi siswa II
DE = FG = jarak siswa I dan siswa II
BC ke DG adalah jarak tiang bendera ke siswa I
Misalkan kita buat segitiga di atas menjadi 2 bagian yaitu segitiga ABG dan segitiga ABF. Karena yang kita cari adalah tinggi tiang listrik, maka kita akan mengarahkan untuk mencari AB
1. Segitiga ABG
2. Segitiga ABF
Perhatikan Kembali uraian segitiga ABG, AB = x √3, jadi tinggi AB = 5√3
Sehingga tinggi tiang bendera:
Daftar pusaka :
1. https://mathcyber1997.com/soal-dan-pembahasan-aplikasi-trigonometri/
2. https://mathematics4us.com/masalah-kontekstual-mengenai-perbandingan-trigonometri-pada-segitiga-siku-siku-sudut-elevasi-dan-sudut-depresi/



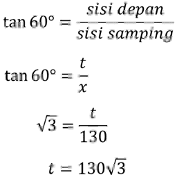















Komentar
Posting Komentar