Komposisi Fungsi dan Invers Fungsi

 1. Fungsi Invers

Fungsi adalah relasi dari himpunan A ke himpunan B jika setiap anggota himpunan A berpasangan dengan tepat satu anggota himpunan B. Dalam pembahasan relasi dan fungsi, himpunan yang terlibat digolongkan ke dalam tiga jenis daerah. 

1. Daerah asal (domain)

Dalam hal ini, himpunan A adalah daerah asal (domain)

2. Daerah kawan (kodomain)

Dalam hal ini, himpunan B adalah daerah kawan (kodomain)

3. Daerah hasil (range fungsi)

Daerah dari hasil dari pemetaan antara domain dan kodomain

Secara umum, himpunan ketiga daerah tersebut dapat dilihat pada gambar di bawah.

Jadi, dari diagram panah di atas dapat disimpukan:

Daerah asal atau Domain adalah A = {1,2,3,4}

Daerah kawan atau Kodomain adalah B = {a,b,c,d,e}

Daerah hasil atau Range fungsi = {a,b,d,e}

Sebuah fungsi dapat dinotasikan dengan huruf kecil sepeti f, g, h. Simbol fungsi yang memetakan himpunan A ke B adalah

f: A → B

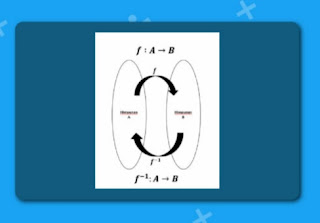
Suatu fungsi f memiliki fungsi invers (kebalikan) f−1 jika f merupakan fungsi satu-satu dan fungsi pada (bijektif). Hubungan tersebut dapat dinyatakan sebagai berikut:

(f-¹)−1=f

Sederhananya, fungsi bijektif berlangsung pada saat jumlah anggota domain sama dengan jumlah anggota kodomain.

Misalkan f fungsi yang memetakan x ke y, sehingga dapat ditulis y = f(x), maka f−¹ adalah fungsi yang memetakan y ke x, ditulis x =f−¹(y). Sebagai contoh f : A→B fungsi bijektif. Invers dari fungsi f adalah fungsi yang mengawankan setiap elemen B dengan tepat satu elemen pada A. Invers dari fungsi f dinyatakan dengan f−¹ seperti di bawah ini:

Terdapat tiga langkah untuk menentukan invers dari suatu fungsi, yaitu:

1. Ubahlah bentuk y = f(x) menjadi bentuk x = f(y).

2. Tuliskan x sebagai f−¹ (y) sehingga f−¹ (y) = f(y).

3. Ubahlah variabel y dengan x sehingga diperoleh rumus fungsi invers (f−¹) (x).

Misalkan, diketahui f(x)=2x+8. Akan dicari fungsi inversnya :

2. Fungsi Komposisi

Fungsi komposisi merupakan suatu penggabungan operasi pada dua jenis fungsi f (x) dan g (x) sampai menghasilkan fungsi baru. Operasi fungsi komposisi biasa yaitu dilambangkan dengan “o” dan dibaca dengan komposisi atau bundaran.

Misalkan fungsi

f :A→B ditentukan dengan rumus y=fx 

g :B→C ditentukan dengan rumus y=gx

Fungsi komposisi dan ditentukan dengan aturan:

h(x)=(g∘f)(x)=g(f(x))

Hal ini dapat diperjelas dengan gambar berikut.

Syarat fungsi g dan f dapat dikomposisikan (g∘f) atau (f∘g) ada, jika daerah hasil dari f adalah himpunan bagian dari daerah asal dari g, yaitu f(A)⊆Dg. Sifat-sifat Fungsi Komposisi adalah sebagai berikut.

a. Pada umumnya, komposisi fungsi tidak bersifat komutatif.

(f∘g) (x) ≠ (g∘f)(x)

b. Komposisi fungsi bersifat assosiatif

Untuk sebarang fungsi f(x), g(x), dan h(x) berlaku sifat assosiatif.

(f∘(g∘h))(x)=((f∘g)∘h)(x)

c. Dalam komposisi fungsi terdapat unsur identitas, yaitu fungsi identitas I(x)=(x) yang memiliki sifat

(f∘I)(x)=(I∘f)(x)=f(x)